Capítulos
El cálculo de distancia entre dos puntos es una herramienta esencial en diversos campos, desde la geometría hasta la navegación y la ciencia de datos. Nos permite medir la separación entre dos ubicaciones en un espacio, ya sea en un plano bidimensional o en un espacio tridimensional. Esta noción de distancia no solo es fundamental en matemáticas, sino que también tiene aplicaciones prácticas en el mundo real, como calcular la distancia entre ciudades en un mapa, determinar la proximidad entre objetos en un espacio tridimensional o incluso evaluar similitudes entre conjuntos de datos.
Ya sea que te sumerjas en el mundo de las coordenadas cartesianas en el plano o que explores las dimensiones más allá, el cálculo de distancia entre dos puntos te proporcionará una base sólida para comprender las relaciones espaciales y aplicar tus conocimientos en una variedad de disciplinas. ¡Comencemos a medir distancias y a explorar la importancia de este concepto fundamental!
Distancia entre dos puntos
Para estudiar la distancia entre dos punto consideremos la siguiente figura.
En la figura podemos encontrar dos puntos 
y 
en el plano cartesiano unidos por un vector. La magnitud del vector coloreado en rojo y que une los puntos, es el valor que representa distancia entre los puntos y .
Fórmula para calcular la distancia entre dos puntos y el teorema de Pitágoras
La fórmula para calcular dicha magnitud está dada por la siguiente expresión:
El valor de esta fórmula puede ser obtenido usando el Teorema de Pitagoras. Para ello, consideremos el triángulo rectángulo de vértices
, y 
.
Notemos que el valor de la hipotenusa de este triángulo es la distancia entre los puntos
y .
Ya que la magnitud de los segmentos que unen y , y son 
y 
respectivamente.
El Teorema de Pitagoras afirma que el valor de la hipotenusa o la distancia entre
y es 
Ejemplos de distancia entre dos puntos
1 Calcular la distancia entre los puntos: 
y 
2 Determinar la condición para que los puntos 
y 
disten una unidad.
Si la distancia entre 
y 
es uno, esto quiere decir que
elevando al cuadrado para eliminar la raiz
3 Probar que los puntos: 
, 
y 
pertenecen a una circunferencia de centro 
.
Si 
es el centro de la circunferencia, para que 
y 
pertenezcan a una circunferencia, por definición las distancias de a , a y a deben ser iguales. Comprobemos esto utilizando la fórmula de la distancia entre dos puntos.
4Clasificar el triángulo determinado por los puntos: 
, 
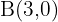y 
Primero calculemos las distancias entre los puntos del triángulo para poder clasificar su tipo.
Ya que 
, podemos concluir que el triángulo no es equilátero, pues si lo fuera, las distancias entre cualesquiera de sus puntos serían iguales.
Además si:
entonces el triángulo es Acutángulo,
cuando 
el triángulo es Rectángulo,
y finalmente, si 
se tiene que el triángulo es Obtusángulo.
Por lo anterior se sigue que
y por lo tanto el triángulo es Obtusángulo.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Suma de vectores f1=450n,30. 1FR=f1+f6
como sacar el residuo de una multiplicación
Hallar las coordenadas de punto medio del segmento que une (4,7);(14,12)
Hola, podrias mencionar que tipo de multiplicación (normal, de vectores etc.).
si se aplica una traslación al punto E(0;2) se obtiene el punto E'(-1;-5),indicar el vector de translación
Sea el vector A= 10 cm y el angulo formado con el eje x es de 50° hallar las componentes del vector analítico y grafico
Encontraste l distancia entre los puntos A 3,5 y B 8,10
Cuál es la fuerza resultante de la magnitud , si f1 es 40 newton y 90 grados y f2 es 30 newton y 0 grados?
23
Mi casa se encuentra ubicada en el punto M(8, 3) y la escuela donde estudio se encuentra ubicada en N(-5, 7). ¿Cuál es la distancia entre mi casa (M) y la Escuela (N)