Un ángulo diedro está formado por dos planos secantes 
Los planos bisectores de un ángulo diedro son el lugar geométrico de los puntos del espacio que equidistan de las caras del diedro .
ecuación de plano bisector
Para encontrar las ecuaciones de los planos bisectores realizamos los pasos:
1La distancia de un punto 
en el plano bisector a cada una de las caras del diedro , es la misma
2Escribimos en términos de 
3Existen dos planos bisectores:
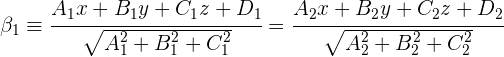
4Simplificamos y obtenemos las ecuaciones de los planos bisectores.
 
Ejemplo
Hallar los planos bisectores del diedro cuyas caras son los planos 
1La distancia de un punto en el plano bisector a cada una de las caras del diedro , es la misma
2Escribimos en términos de
3Existen dos planos bisectores:
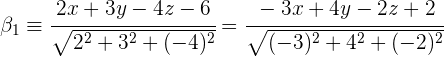
4Simplificamos y obtenemos las ecuaciones de los planos bisectores.
Para el primer plano bisector tenemos
 
Para el segundo plano bisector tenemos
 
5Las ecuaciones de los planos bisectores son:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
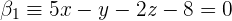
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Buenas, cómo calculas el volumen del paralelepípedo si te aparecen los vectores u(2,1,0)^t , v(1,2,2)^t, w(-1,0,2)^t ?
¿Por qué en el calculo de la distancia punto recta, el orden de la matriz és alterado?
Hola podrías mencionar un ejemplo pues no encuentro la alteración que mencionas, solo veo que se sigue la fórmula que se indica.
No me queda claro por qué el área de un paralelogramo con los vectores ā y ē es |ā x ē| en vez de ser |ā|·|ē| que sería el módulo (longitud) de uno por el módulo (longitud) del otro.
Para entenderlo recordemos cómo se calcula el área del paralelogramo es base por altura, para la base se toma el módulo de uno de los vectores pero para altura se toma la proyección del otro vector en el eje vertical lo que implica la función seno y ya multiplicados dan una de las definiciones del producto cruz, en el artículo «https://www.superprof.es/apuntes/escolar/matematicas/analitica/distancias/areas-y-volumenes.html#tema_area-del-paralelogramo» se la imagen de lo que explique.